Home » Subject » Combinatorics

Long rainbow arithmetic progressions

Importance: Medium ✭✭
Author(s): Fox, Jacob
Jungic, Veselin
Mahdian, Mohammad
Nesetril, Jaroslav
Radoicic, Rados
Subject: Combinatorics
Keywords: arithmetic progression
rainbow
Recomm. for undergrads: no
Posted by: vjungic
on: July 3rd, 2007

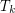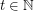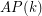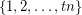For $ k\in \mathbb{N} $ let $ T_k $ denote the minimal number $ t\in \mathbb{N} $ such that there is a rainbow $ AP(k) $ in every equinumerous $ t $-coloring of $ \{ 1,2,\ldots ,tn\} $ for every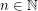 $ n\in \mathbb{N} $

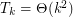Conjecture   For all $ k\geq 3 $, $ T_k=\Theta (k^2) $.

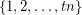A $ t $-coloring of $ \{ 1,2,\ldots, tn\} $ is equinumerous if each color is used $ n $ times. An arithmetic progression is rainbow if it does not containt two terms of the same color.

In [JLMNR] it was proved that 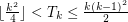$ \lfloor \frac{k^2}{4}\rfloor <T_k\leq \frac{k(k-1)^2}{2} $.

It is known that 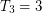$ T_3=3 $ ([AF], [JR]) and 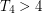$ T_4 > 4 $ ([CJR]). It is not hard to show that 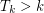$ T_k > k $ for all 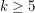$ k\ge 5 $ ([AF]).

Related problems

Rainbow AP(4) in an almost equinumerous coloring

Bibliography

[AF] Maria Axenovich, Dmitri Fon-Der-Flaass: On rainbow arithmetic progressions, Electronic Journal of Combinatorics, 11, (2004), R1.

[CJR] David Conlon, Veselin Jungic, Rados Radoicic, On the existence of rainbow 4-term arithmetic progressions, Graphs and Combinatorics, 23 (2007), 249-254

*[JLMNR] Veselin Jungic, Jacob Licht (Fox), Mohammad Mahdian, Jaroslav Nesetril, Rados Radoicic : Rainbow arithmetic progressions and anti-Ramsey results, Combinatorics, Probability, and Computing - Special Issue on Ramsey Theory, 12, (2003), 599--620.

[JNR] Veselin Jungic, Jaroslav Nesetril, Rados Radoicic: Rainbow Ramsey theory, Integers, The Electronic Journal of Combinatorial Number Theory, Proceedings of the Integers Conference 2003 in Honor of Tom Brown, 5(2), (2005), A9.

[JR] Veselin Jungic, Rados Radoicic : Rainbow 3-term arithmetic progressions, Integers, The Electronic Journal of Combinatorial Number Theory, 3, (2003), A18.


* indicates original appearance(s) of problem.
add new comment

Is this unsolved?

On May 12th, 2010 Anonymous says:

Looks like a nice problem, but is it still unsolved?

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.