 login/create account
login/create account
Radoicic, Rados
Long rainbow arithmetic progressions ★★
Author(s): Fox; Jungic; Mahdian; Nesetril; Radoicic
For  let
let 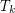 denote the minimal number
denote the minimal number 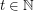 such that there is a rainbow
such that there is a rainbow 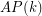 in every equinumerous
in every equinumerous 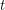 -coloring of
-coloring of 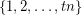 for every
for every 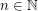
Conjecture For all  ,
, 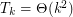 .
.
 ,
, 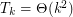 .
. Keywords: arithmetic progression; rainbow

 Drupal
Drupal CSI of Charles University
CSI of Charles University