 login/create account
login/create account
Crossing sequences
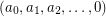 be a sequence of nonnegative integers which strictly decreases until
be a sequence of nonnegative integers which strictly decreases until  .
.
Then there exists a graph that be drawn on a surface with orientable (nonorientable, resp.) genus  with
with 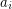 crossings, but not with less crossings.
crossings, but not with less crossings.
This actually are two conjectures, one for the orientable case and another for nonorientable one. For sequences 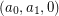 the nonorientable case was resolved in [ABS] and the orientable one in [DMS].
the nonorientable case was resolved in [ABS] and the orientable one in [DMS].
The conclusion also holds (for the orientable case) whenever the sequence 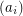 is convex [S], that is whenever
is convex [S], that is whenever 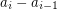 is nonincreasing. It might seem that this condition is also necessary: For the most extreme sequence
is nonincreasing. It might seem that this condition is also necessary: For the most extreme sequence 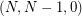 (suggested by Salazar) one needs to construct a graph for which adding one handle saves just one crossing, while adding another saves many -- but then why not add the second handle first? Somewhat surprisingly, graphs with this counterintuitive property exist, at least for sequences
(suggested by Salazar) one needs to construct a graph for which adding one handle saves just one crossing, while adding another saves many -- but then why not add the second handle first? Somewhat surprisingly, graphs with this counterintuitive property exist, at least for sequences 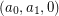 .
.
An interesting open case is to consider sequences for which 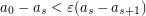 for some
for some  and small
and small  .
.
Bibliography
*[ABS] Dan Archdeacon, C. Paul Bonnington, and Jozef Siran, Trading crossings for handles and crosscaps, J.Graph Theory 38 (2001), 230--243.
[DMS] Matt DeVos, Bojan Mohar, Robert Samal, Unexpected behaviour of crossing sequences, in preparation
[S] Jozef Siran, The crossing function of a graph, Abh. Math. Sem. Univ. Hamburg 53 (1983), 131--133.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University