 login/create account
login/create account
For a graph  , let
, let 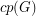 denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let
denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 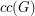 denote the cardinality of a minimum feedback vertex set (set of vertices
denote the cardinality of a minimum feedback vertex set (set of vertices 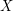 so that
so that 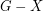 is acyclic).
is acyclic).
 ,
, 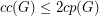 .
. In [KLL], the authors mention that there exists a family of nonplanar graphs for which 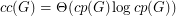 , so no such result could hold for general graphs. They also point out that the conjecture is tight for wheels, and they prove it for the special case of outerplanar graphs.
, so no such result could hold for general graphs. They also point out that the conjecture is tight for wheels, and they prove it for the special case of outerplanar graphs.
Bibliography
*[KLL] Ton Kloks, Chuan-Min Lee, and Jiping Liu, New Algorithms for  -Face Cover,
-Face Cover,  -Feedback Vertex Set, and
-Feedback Vertex Set, and  -Disjoint Cycles on Plane and Planar Graphs, in Proceedings of the 28th International Workshop on Graph-Theoretic Concepts in Computer Science (WG2002), LNCS 2573, pp. 282--295, 2002.
-Disjoint Cycles on Plane and Planar Graphs, in Proceedings of the 28th International Workshop on Graph-Theoretic Concepts in Computer Science (WG2002), LNCS 2573, pp. 282--295, 2002.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University