 login/create account
login/create account
An oriented colouring of an oriented graph is assignment  of colours to the vertices such that no two arcs receive ordered pairs of colours
of colours to the vertices such that no two arcs receive ordered pairs of colours 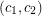 and
and 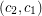 . It is equivalent to a homomorphism of the digraph onto some tournament of order
. It is equivalent to a homomorphism of the digraph onto some tournament of order  .
.
Raspaud and Sopena [RS] showed using Borodin's result about acyclic chromatic number of planar graphs, that every planar oriented graph has oriented chromatic number at most 80. (Their motivation came from a work of Courcelle [C] concerning the monadic second-order logic of graphs. That, however, deals with a stronger variant of coloring.)
On the other hand, Marshall [M] showed that there is an oriented planar graph with oriented chromatic number at least~17.
Bibliography
[C] B. Courcelle, The monadic second order logic of graphs VI: On several representations of graphs by relational structures, Discrete Appl. Math. 54 ( 1994),
[M] T. H. Marshall. On  -universal graphs. Research Report 2001-510, KAM-DIMATIA Series, 2001.
-universal graphs. Research Report 2001-510, KAM-DIMATIA Series, 2001.
*[RS] A. Raspaud and E. Sopena. Good and semi-strong colorings of oriented planar graphs. Inform. Process. Lett., 51(4):171–174, 1994. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University