 login/create account
login/create account
 such that the list chromatic number of any bipartite graph
such that the list chromatic number of any bipartite graph  of maximum degree
of maximum degree 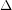 is at most
is at most 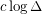 .
.
For definitions and an introduction to list colouring, see the related Wikipedia page.
Alon [A] showed that the list chromatic number of a graph (not necessarily bipartite) of maximum degree 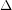 is at least
is at least 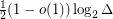 . Random bipartite graphs show that this is tight up to a multiplicative factor
. Random bipartite graphs show that this is tight up to a multiplicative factor 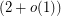 .
.
It is not diffcult to see that the list chromatic number of any bipartite graph  of maximum degree
of maximum degree 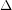 is at most
is at most 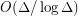 . It also follows a more general result of Johansson [J] on triangle-free graphs.
. It also follows a more general result of Johansson [J] on triangle-free graphs.
Bibliography
*[A] N. Alon, Degrees and choice numbers, Random Structures Algorithms, 16 (2000), 364--368.
[AK] N. Alon and M. Krivelevich, The choice number of random bipartite graphs, Annals of Combi- natorics 2 (1998), 291-297.
[J] A. Johansson. Asymptotic choice number for triangle free graphs. Technical Report 91–95, DIMACS, 1996.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University