 login/create account
login/create account
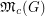 always rational?
always rational? Given a proper  -colouring
-colouring  of a graph
of a graph  , consider the following 'mixing process:'
, consider the following 'mixing process:'
- \item choose a vertex
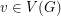 ; \item change the colour of
; \item change the colour of  (if possible) to yield a different
(if possible) to yield a different  -colouring
-colouring 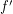 of
of  .
. A natural problem arises: Can every  -colouring of
-colouring of  be generated from
be generated from  by repeatedly applying this process? If so, we say that
by repeatedly applying this process? If so, we say that  is
is  -mixing.
-mixing.
The problem of determining if a graph is  -mixing and several related problems have been studied in a series of recent papers [1,2,4-6]. The authors of [4] provide examples which show that a graph can be
-mixing and several related problems have been studied in a series of recent papers [1,2,4-6]. The authors of [4] provide examples which show that a graph can be  -mixing but not
-mixing but not 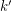 -mixing for integers
-mixing for integers 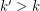 . For example, given
. For example, given 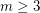 consider the bipartite graph
consider the bipartite graph 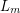 which is obtained by deleting a perfect matching from
which is obtained by deleting a perfect matching from 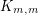 . It is an easy exercise to show that for
. It is an easy exercise to show that for 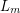 is
is  -mixing if and only if
-mixing if and only if 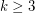 and
and 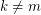 . This example motivates the following definition.
. This example motivates the following definition.
 to be
to be 
An analogous definition can be made for circular colouring. Recall, a 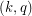 -colouring of a graph is a mapping
-colouring of a graph is a mapping 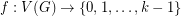 such that if
such that if 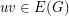 , then
, then 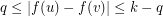 . As with ordinary colourings, we say that a graph
. As with ordinary colourings, we say that a graph  is
is 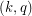 -mixing if all
-mixing if all 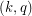 -colourings of
-colourings of  can be generated from a single
can be generated from a single 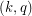 -colouring
-colouring  by recolouring one vertex at a time.
by recolouring one vertex at a time.
 to be
to be 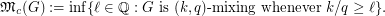
Several bounds on the circular mixing threshold are obtained in [3], including the following which relates the circular mixing threshold to the mixing threshold.
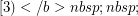 ] For every graph
] For every graph  ,
, 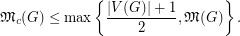
As a corollary, we have the following: if 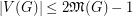 , then
, then 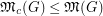 . However, examples in [3] show that the ratio
. However, examples in [3] show that the ratio 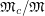 can be arbitrarily large in general.
can be arbitrarily large in general.
Regarding the problem of determining if 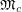 is rational, it is worth mentioning that there are no known examples of graphs
is rational, it is worth mentioning that there are no known examples of graphs  for which
for which 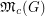 is not an integer.
is not an integer.
Other problems are also given in [3]. One can check that 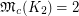 and
and 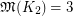 . However, the only graphs which are known to satisfy
. However, the only graphs which are known to satisfy 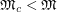 are in some sense related to
are in some sense related to 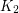 , eg. trees and complete bipartite graphs.
, eg. trees and complete bipartite graphs.
 such that
such that 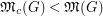 ?
? Using an example from [4], it is shown in [3] that if 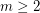 is an integer, then there is a graph
is an integer, then there is a graph  such that
such that 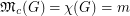 if and only if
if and only if 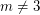 . A natural question to ask is whether a similar result holds for the circular chromatic number. Again, certain bipartite graphs are an exception.
. A natural question to ask is whether a similar result holds for the circular chromatic number. Again, certain bipartite graphs are an exception.
 such that
such that 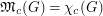 ?
? Also, the example of 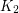 shows that the circular mixing threshold is, in general, not attained. However, the following problem is open.
shows that the circular mixing threshold is, in general, not attained. However, the following problem is open.
For more precise versions of the last three questions, see [3].
Bibliography
[1] P. Bonsma and L. Cereceda. Finding paths between graph colourings: PSPACE-completeness and superpolynomial distances. Theoret. Comput. Sci. 410 (2009), (50): 5215--5226.
[2] P. Bonsma, L. Cereceda, J. van den Heuvel, and M. Johnson. Finding paths between graph colourings: Computational complexity and possible distances. Electronic Notes in Discrete Mathematics 29 (2007): 463--469.
*[3] R. C. Brewster and J. A. Noel. Mixing Homomorphisms and Extending Circular Colourings. Submitted. pdf.
[4] L. Cereceda, J. van den Heuvel, and M. Johnson. Connectedness of the graph of vertex-colourings. Discrete Math. 308 (2008), (5-6): 913--919.
[5] L. Cereceda, J. van den Heuvel, and M. Johnson. Mixing 3-colourings in bipartite graphs. European J. Combin. 30 (2009), (7): 1593--1606.
[6] L. Cereceda, J. van den Heuvel, and M. Johnson. Finding paths between 3-colorings. Journal of Graph Theory, 67 (2011), (1): 69--82.
[7] J. A. Noel. "Jonathan Noel - Mixing Circular Colourings." Webpage.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University