Open Problem Garden

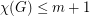This conjecture may be viewed as a bipartite analogue of the Erdos-Faber-Lovasz Conjecture.

One very special case of this conjecture is the statement that a complete graph on 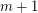vertices cannot be written as a disjoint union of fewer than complete bipartite graphs (although it does have numerous such decompositions). This was proved by Graham and Pollak [GP] who used spectral techniques to establish the following stronger fact.

Theorem   Let be a simple loopless graph, and assume that the adjacency matrix of has positive and 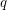negative eigenvalues. If 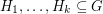is a list of edge disjoint subgraphs with union and each 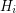is a complete bipartite graph, then .

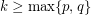Alternative proofs of the Graham-Pollak Theorem have been found by [P] and [T], and Alon, Brualdi, and Schader [ABS] resolved a conjecture of de Caen by proving that whenever 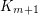is edge-colored so that each color class induces a complete bipartite graph, there is a spanning tree with one edge of each color. However, all of these results depend heavily on spectral tools. A proof of the general conjecture would appear to either require a vast generalization of these techniques, or a new combinatorial proof of the Graham-Pollak Theorem.