Home » Subject » Geometry
Importance: High ✭✭✭
Author(s): Kneser, M.
Poulsen, E. T.
Subject: Geometry
Keywords: pushing disks
Recomm. for undergrads: no
Posted by: tchow
on: September 25th, 2008
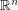Conjecture   If a finite set of unit balls in $ \mathbb{R}^n $ is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease.

This problem dates from the mid-1950's. The planar case was solved by Bezdek and Connelly in 2003, who also showed that the area of the intersection does not increase, and that the result holds even if the disks have unequal radii. In higher dimensions the problem remains open.

The conjecture is known to hold if the rearrangement can be executed by a continuous motion such that the distance between every pair of centers monotonically increases throughout the motion.

Bibliography

*[BC] K. Bezdek and R. Connelly, Pushing disks apart: The Kneser-Poulsen conjecture in the plane, J. Reine Angew. Math. 553 (2002), 221--236.

*[K] M. Kneser, Einige Bemerkungen über das Minkowskische Flächenmass, Arch. Math. 6 (1955), 382--390.

*[P] E. T. Poulsen, Problem 10, Math. Scand. 2 (1954), 346.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options