 login/create account
login/create account
pushing disks
Kneser–Poulsen conjecture ★★★
Conjecture If a finite set of unit balls in 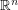 is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease.
is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease.
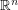 is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease.
is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease. Keywords: pushing disks

 Drupal
Drupal CSI of Charles University
CSI of Charles University