 login/create account
login/create account
Conjecture An integer partition is wide if and only if it is Latin.
An integer partition 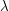 is wide if
is wide if 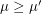 for every subpartition
for every subpartition 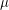 of
of 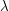 . (Here
. (Here 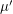 denotes the conjugate of
denotes the conjugate of 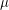 ,
, 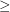 denotes dominance or majorization order, and a subpartition of
denotes dominance or majorization order, and a subpartition of 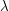 is a submultiset of the parts of
is a submultiset of the parts of 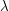 .) An integer partition
.) An integer partition 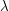 is Latin if there exists a tableau
is Latin if there exists a tableau 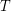 of shape
of shape 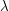 such that for every
such that for every  , the
, the  th row of
th row of 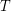 contains a permutation of
contains a permutation of 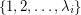 , and such that every column of
, and such that every column of 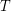 contains distinct integers. It is easy to show that if
contains distinct integers. It is easy to show that if 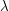 is Latin then
is Latin then 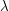 is wide, but the converse remains open.
is wide, but the converse remains open.
Bibliography
*[CFGV] Timothy Y. Chow, C. Kenneth Fan, Michel X. Goemans, Jan Vondrak, Wide partitions, Latin tableaux, and Rota's basis conjecture, Advances Appl. Math. 21 (2003), 334-358.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University