 login/create account
login/create account
category theory
A conjecture about direct product of funcoids ★★
Author(s): Porton
Conjecture Let 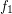 and
and 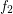 are monovalued, entirely defined funcoids with
are monovalued, entirely defined funcoids with 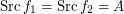 . Then there exists a pointfree funcoid
. Then there exists a pointfree funcoid 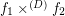 such that (for every filter
such that (for every filter  on
on  )
) 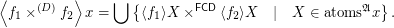 (The join operation is taken on the lattice of filters with reversed order.)
(The join operation is taken on the lattice of filters with reversed order.)
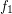 and
and 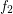 are monovalued, entirely defined funcoids with
are monovalued, entirely defined funcoids with 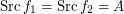 . Then there exists a pointfree funcoid
. Then there exists a pointfree funcoid 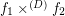 such that (for every filter
such that (for every filter  on
on  )
) 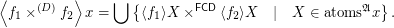 (The join operation is taken on the lattice of filters with reversed order.)
(The join operation is taken on the lattice of filters with reversed order.) A positive solution of this problem may open a way to prove that some funcoids-related categories are cartesian closed.
Keywords: category theory; general topology

 Drupal
Drupal CSI of Charles University
CSI of Charles University