 login/create account
login/create account
Magic square of squares
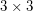 magic square composed of distinct perfect squares?
magic square composed of distinct perfect squares? This question was first asked in 1984 by Martin LaBar and popularized in 1996 by Martin Gardner, who offered $100 to the first person to construct such a square. In 2005 Christian Boyer offered €1,000 and a bottle of champagne for a solution to a somewhat easier problem [Bc]. For a review of the history of research, see [Ba, Bb, Bc]. For basic facts about the anticipated 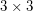 magic square of squares, see [Br, Mo].
magic square of squares, see [Br, Mo].
Bibliography
[Ba] Christian Boyer. Some notes on the magic squares of squares problem. The Mathematical Intelligencer 27 (2005), 2, 52-64.
[Bb] Christian Boyer. Magic squares of squares, "Multimagic Squares" website.
[Bc] Christian Boyer. Latest research on the "3x3 magic square of squares" problem, "Multimagic Squares" website.
[Br] Kevin Brown. Magic Square of Squares, "Math Pages" website.
[Mo] Lee Morgenstern. 3x3 Magic Square of Squares Formulations
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University