 login/create account
login/create account
Directed path of length twice the minimum outdegree
Conjecture Every oriented graph with minimum outdegree  contains a directed path of length
contains a directed path of length 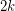 .
.
 contains a directed path of length
contains a directed path of length 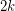 .
. In fact, Thomassé made the following stronger conjecture which implies the celebrated Cacetta-Häggkvist Conjecture.
Conjecture Every digraph with minimum outdegree  and directed girth
and directed girth  , contains a directed path of length
, contains a directed path of length 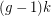 .
.
 and directed girth
and directed girth  , contains a directed path of length
, contains a directed path of length 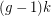 .
. This conjecture holds easily when 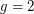 . For
. For 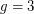 it is the above conjecture which is still open.
it is the above conjecture which is still open.
Bibliography
*[S] Blair D. Sullivan: A Summary of Problems and Results related to the Caccetta-Haggkvist Conjecture
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University