Home » Subject » Graph Theory » Directed Graphs

Cyclic spanning subdigraph with small cyclomatic number

Importance: Medium ✭✭
Author(s): Bondy, J. Adrian
Subject: Graph Theory
» Directed Graphs
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: June 2nd, 2013
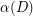Conjecture   Let $ D $ be a digraph all of whose strong components are nontrivial. Then $ D $ contains a cyclic spanning subdigraph with cyclomatic number at most $ \alpha(D) $.

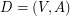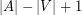The {\it cyclomatic number} of a digraph $ D=(V,A) $ is $ |A|-|V|+1 $. For a strong digraph, it correspond to the minimum of directed ears in a directed ears decomposition. (See Chapter 5 of [BM]).

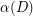$ \alpha(D) $ denotes the {\it stability number} of the digraph $ D $, that is the maximum number of pairwise non-adjacent vertices.

Bessy and Thomassé [BT04] showed that any nontrivial strong digraph $ D $ has a spanning subdigraph which is the union of $ \alpha $ directed cycles. However, the structure of this subdigraph might be rather complicated. This leads one to ask whether there always exists a spanning subdigraph whose structure is relatively simple, one which is easily seen to be the union of $ \alpha $ directed cycles. 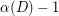A natural candidate would be a spanning subdigraph built from a directed cycle by adding $ \alpha(D)-1 $ directed ears. 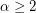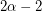But or any $ \alpha \geq 2 $, there exists a digraph $ D $ with stability number $ \alpha $ requiring at least $ 2\alpha -2 $ directed ears. See Chapter 19 of [BM08].

A possible way around this problem is to allow spanning subdigraphs which are disjoint union of strong digraphs. Such digraph are called cyclic (because each arc lies on a directed cycle). The conjecture was formulated by Bondy[B], based on a remark of Chen and Manalastas [CM].

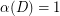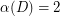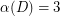The Conjecture holds for $ \alpha(D)=1 $ by Camion's Theorem [C] and also for $ \alpha(D)=2 $ and $ \alpha(D)=3 $ by theorems of Chen and Manalastas [CM] and S. Thomassé (unpublished), respectively.

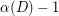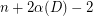The conjecture implies not only the above-mentioned Bessy--Thomassé Theorem, but also a result of Thomassé [Thom01], that the vertex set of any strong digraph $ D $ with $ \alpha(D) \geq 2 $ can be partitioned into $ \alpha(D)-1 $ directed paths, as well as another theorem of Bessy and Thomassé [BT03], that every strong digraph $ D $ has a strong spanning subdigraph with at most $ n+2\alpha(D)-2 $ arcs.

Bibliography

[BT03] S. Bessy and S. Thomassé, Every strong digraph has a spanning strong subgraph with at most 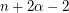$ n+2\alpha-2 $ arcs. J. Combin. Theory Ser. B 87 (2003), 289--299.

[BT04] S. Bessy and S. Thomassé, Three min-max theorems concerning cyclic orders of strong digraphs. In Integer Programming and Combinatorial Optimization, 132--138. Lecture Notes in Comput. Sci., Vol. 3064, Springer, Berlin.

*[B95] J.A. Bondy, Basic graph theory: paths and circuits. In Handbook of Combinatorics, Vol. 1, 3--110. Elsevier, Amsterdam.

[BM] J.A. Bondy and U.S.R. Murty, Graph Theory, volume 244 of Graduate Texts in Mathematics. Springer, 2008.

[C] P. Camion, Chemins et circuits hamiltoniens des graphes complets. C. R. Acad. Sci. Paris 249 (1959), 2151--2152.

[CM] C.C. Chen C.C. and Jr. P. Manalastas, Every finite strongly connected digraph of stability 2 has a Hamiltonian path. Discrete Math. 44 (1983), 243--250.

[T] S. Thomassé, Covering a strong digraph by 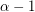$ \alpha-1 $ disjoint paths: a proof of Las Vergnas' conjecture. J. Combin. Theory Ser. B 83 (2001), 331--333.


* indicates original appearance(s) of problem.
add new comment