 login/create account
login/create account
Criterion for boundedness of power series
Question Give a necessary and sufficient criterion for the sequence 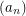 so that the power series
so that the power series 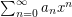 is bounded for all
is bounded for all 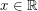 .
.
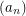 so that the power series
so that the power series 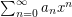 is bounded for all
is bounded for all 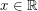 .
. Consider a power series 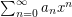 that is convergent for all
that is convergent for all 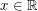 , thus defining a function
, thus defining a function 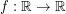 . Are there criteria to decide whether
. Are there criteria to decide whether  is bounded (which e.g. is the case for the series with
is bounded (which e.g. is the case for the series with 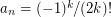 for
for 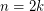 and
and 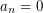 for n odd)? Some general remarks:
for n odd)? Some general remarks:
- \item A necessary condition for
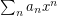 to be bounded is that
to be bounded is that 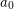 is the only non-zero
is the only non-zero 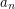 or there are infinitely many non-zero
or there are infinitely many non-zero 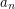 's which change sign infinitely many times. \item Changing a finite set of
's which change sign infinitely many times. \item Changing a finite set of 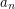 's (except
's (except 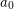 ) does leave the subspace of bounded power series. \item The subspace of bounded power series is "large" in the sense that it is both a linear subspace (closed under sums and scalar multiples) and an algebra (closed under products). It includes all functions of the form
) does leave the subspace of bounded power series. \item The subspace of bounded power series is "large" in the sense that it is both a linear subspace (closed under sums and scalar multiples) and an algebra (closed under products). It includes all functions of the form 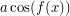 , where
, where  is any entire function
is any entire function 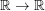 . The question whether the subspace of bounded power series contains only these functions seems to be open.
. The question whether the subspace of bounded power series contains only these functions seems to be open. What you have then is a
On June 21st, 2012 Anonymous says:
What you have then is a polynomial, and any nonconstant polynomial function is unbounded.
Re: A necessary condition
On February 16th, 2011 Comet says:
I posted the above comment anonymously, but now I have created an account. "It seems the sum would be bounded if there are only finitely many non-zero a sub n; it is not apparent to me that a sub 0 be the only non-zero a sub n."
sin x = cos(pi/2 - x)
On June 21st, 2012 Anonymous says:
The sine function is in the class mentioned.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A necessary condition
It seems the sum would be bounded if there are only finitely many non-zero a sub n; it is not apparent to me that a sub 0 be the only non-zero a sub n.