 login/create account
login/create account
Counterexamples to the Baillie-PSW primality test
Problem (1) Find a counterexample to Baillie-PSW primality test or prove that there is no one.
Problem (2) Find a composite 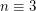 or
or 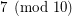 which divides both
which divides both 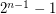 (see Fermat pseudoprime) and the Fibonacci number
(see Fermat pseudoprime) and the Fibonacci number 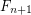 (see Lucas pseudoprime), or prove that there is no such
(see Lucas pseudoprime), or prove that there is no such  .
.
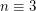 or
or 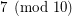 which divides both
which divides both 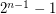 (see Fermat pseudoprime) and the Fibonacci number
(see Fermat pseudoprime) and the Fibonacci number 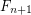 (see Lucas pseudoprime), or prove that there is no such
(see Lucas pseudoprime), or prove that there is no such  .
.
Selfridge, Wagstaff, and Pomerance offered $500 + $100 + $20 for  satisfying Problem 2, and $20 + $100 + $500 for a proof that there is no such
satisfying Problem 2, and $20 + $100 + $500 for a proof that there is no such  (R. Guy, 1994).
(R. Guy, 1994).
Bibliography
Carl Pomerance. "Are There Counterexamples to the Baillie-PSW Primality Test?"
Thomas R. Nicely. " The Baillie-PSW primality test."
R. K. Guy. "Pseudoprimes. Euler Pseudoprimes. Strong Pseudoprimes". §A12 in "Unsolved Problems in Number Theory", 2nd ed. New York: Springer-Verlag, pp. 27-30, 1994.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University