 login/create account
login/create account
Beneš Conjecture (graph-theoretic form)
 ) Find a sufficient condition for a straight
) Find a sufficient condition for a straight  -stage graph to be rearrangeable. In particular, what about a straight uniform graph?
-stage graph to be rearrangeable. In particular, what about a straight uniform graph?  ) Let
) Let  be a simple regular ordered
be a simple regular ordered  -stage graph. Suppose that the graph
-stage graph. Suppose that the graph 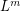 is externally connected, for some
is externally connected, for some 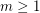 . Then the graph
. Then the graph 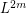 is rearrangeable.
is rearrangeable. Given an integer 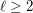 , an
, an  -stage graph is an
-stage graph is an  -partite graph
-partite graph  with a list of its parts
with a list of its parts 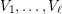 such that every edge of
such that every edge of  has endpoints in both
has endpoints in both 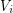 and
and 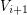 , for some
, for some ![$ i\in[\ell-1] $](/files/tex/87da414aab7edd9032d4b489017cd17095f73803.png) . A vertex in
. A vertex in 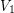 (
(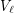 ) is a source (target) of
) is a source (target) of  . A path in
. A path in  is plain if it goes from a source to a target through each part of
is plain if it goes from a source to a target through each part of  exactly once. The graph
exactly once. The graph  is externally connected if for every source
is externally connected if for every source  and target
and target  there exists a plain path from
there exists a plain path from  to
to  . A mask for
. A mask for  is a
is a  -stage multigraph
-stage multigraph  whose sources and targets are exactly those of
whose sources and targets are exactly those of  and such that every vertex of
and such that every vertex of  has the same degree in
has the same degree in  . The graph
. The graph  is rearrangeable if for every its mask there exists a collection, called routing, of corresponding mutually edge-disjoint plain paths in
is rearrangeable if for every its mask there exists a collection, called routing, of corresponding mutually edge-disjoint plain paths in  .
.
The graph  is ordered if each of its parts is linearly ordered. The graph
is ordered if each of its parts is linearly ordered. The graph  is uniform and denoted
is uniform and denoted 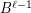 if there is an ordered 2-stage graph
if there is an ordered 2-stage graph  with equal-sized parts such that
with equal-sized parts such that  is the proper (i.e., respecting all the orders in
is the proper (i.e., respecting all the orders in  ) concatenation of
) concatenation of 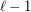 identical copies of
identical copies of  . The graph
. The graph  is straight if for any
is straight if for any 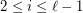 and any
and any 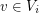 , the number of edges joining
, the number of edges joining  with
with 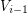 equals that of
equals that of 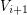 .
.
Conjecture ( ) can be reformulated as
) can be reformulated as 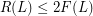 , where
, where 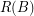 (
(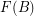 ) denotes the smallest positive integer
) denotes the smallest positive integer  , or
, or  if none exists, such that the graph
if none exists, such that the graph 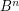 is rearrangeable (externally connected).
is rearrangeable (externally connected).
Examples
Consider the simple 2-regular  -stage ordered graphs
-stage ordered graphs 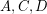 shown in Fig.1. It is easy to see that
shown in Fig.1. It is easy to see that 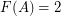 and
and 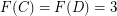 (the corresponding externally connected graphs
(the corresponding externally connected graphs 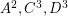 are depicted in blue). Therefore, according to Conjecture (
are depicted in blue). Therefore, according to Conjecture ( ), the graphs
), the graphs 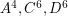 should be rearrangeable, which is indeed the case. The graph
should be rearrangeable, which is indeed the case. The graph  is the 2-stage Shuffle-exchange graph
is the 2-stage Shuffle-exchange graph 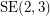 , and there are several nice proofs known for
, and there are several nice proofs known for 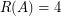 . Although I am not aware of any theoretical proof for rearrangeability of
. Although I am not aware of any theoretical proof for rearrangeability of 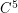 or
or 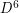 , I have verified by brute force without difficulty that
, I have verified by brute force without difficulty that 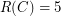 and
and 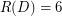 .
.
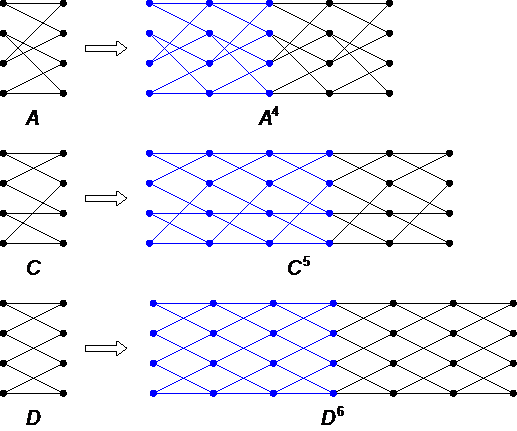
Figure 1. Examples for Conjecture ( ).
).
Link to Beneš Conjecture
Problem ( ) and Conjecture (
) and Conjecture ( ) are equivalent "graph-theoretic" forms of Problem (
) are equivalent "graph-theoretic" forms of Problem ( ) and Beneš conjecture [B75], respectively.
) and Beneš conjecture [B75], respectively.
The equivalence is based on the natural bijection between the  -systems of partitions and the straight
-systems of partitions and the straight  -stage graphs, given any
-stage graphs, given any 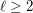 . Here an
. Here an  -system of partitions is an
-system of partitions is an  -tuple
-tuple 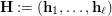 of partitions of some finite set
of partitions of some finite set  . The image of
. The image of  under this bijection is the straight
under this bijection is the straight  -stage graph denoted
-stage graph denoted 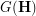 and defined as follows. The edge set of
and defined as follows. The edge set of 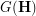 is
is ![$ [\ell-1]\times E $](/files/tex/654d347529db18b97e62d7568dd0c7d15a1b02d5.png) , the
, the  th vertex part is
th vertex part is 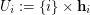 , for all
, for all ![$ i\in[\ell] $](/files/tex/27ff80b603f9b3bd2ea80a83f7c6ab27c26475de.png) , and the edge-vertex incidence is such that every edge
, and the edge-vertex incidence is such that every edge 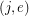 has endpoints
has endpoints 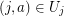 and
and 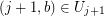 uniquely determined by
uniquely determined by 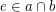 .
.
The bijection 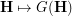 provides a convenient two-way link between the frameworks for Problems (
provides a convenient two-way link between the frameworks for Problems ( ) and (
) and ( ) via numerous easily seen equivalences. Here is some basic ones:
) via numerous easily seen equivalences. Here is some basic ones:
 Simplicity of
Simplicity of 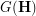 is equivalent to the condition
is equivalent to the condition 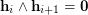 , for all
, for all ![$ i\in[\ell-1] $](/files/tex/87da414aab7edd9032d4b489017cd17095f73803.png) .
.
 Uniformity of
Uniformity of 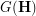 is equivalent to the existence of a permutation
is equivalent to the existence of a permutation  of
of  such that
such that 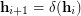 , for all
, for all ![$ i\in[\ell-1] $](/files/tex/87da414aab7edd9032d4b489017cd17095f73803.png) .
.

 -quasi-regularity of
-quasi-regularity of 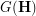 is equivalent to every block of
is equivalent to every block of 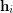 being of size
being of size  , for all
, for all ![$ i\in[\ell] $](/files/tex/27ff80b603f9b3bd2ea80a83f7c6ab27c26475de.png) . Here the graph
. Here the graph  is
is  -quasi-regular if the induced bipartite subgraph on
-quasi-regular if the induced bipartite subgraph on 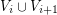 is
is  -regular, for all
-regular, for all ![$ i\in[\ell-1] $](/files/tex/87da414aab7edd9032d4b489017cd17095f73803.png) . Note that a quasi-regular multistage graph is straight. Also,
. Note that a quasi-regular multistage graph is straight. Also,  -quasi-regularity of
-quasi-regularity of 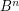 is equivalent to
is equivalent to  -regularity of
-regularity of  .
.
 External connectivity of
External connectivity of 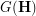 is equivalent to transitivity of
is equivalent to transitivity of 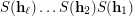 .
.
 Given a permutation
Given a permutation 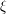 of
of  , the membership
, the membership 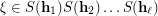 is equivalent to routability of the mask
is equivalent to routability of the mask 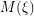 for
for 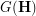 defined as follows. The edge set of
defined as follows. The edge set of 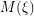 is
is  and the edge-vertex incidence is such that every edge
and the edge-vertex incidence is such that every edge 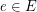 has endpoints
has endpoints 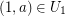 and
and 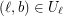 uniquely determined by
uniquely determined by 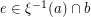 . Note that given
. Note that given  , the map
, the map 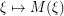 is surjective (but generally not injective).
is surjective (but generally not injective).
 Consequently, rearrangeability of
Consequently, rearrangeability of 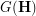 is equivalent to completeness of
is equivalent to completeness of  . Here
. Here  is complete if it satisfies
is complete if it satisfies 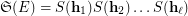 .
.
 If
If 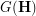 is rearrangeable, then any routing algorithm for
is rearrangeable, then any routing algorithm for 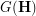 easily translates to a factorization algorithm of the same complexity for the latter identity, and vise versa. Here, given a rearrangeable multistage graph, a routing algorithm is one that takes a mask of the graph as input and returns a corresponding routing.
easily translates to a factorization algorithm of the same complexity for the latter identity, and vise versa. Here, given a rearrangeable multistage graph, a routing algorithm is one that takes a mask of the graph as input and returns a corresponding routing.
 Contracting all edges between
Contracting all edges between 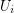 and
and 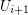 in
in 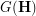 is equivalent to replacing the partitions
is equivalent to replacing the partitions 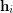 and
and 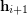 in
in  with their supremum
with their supremum 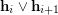 , given any fixed
, given any fixed ![$ i\in[\ell-1] $](/files/tex/87da414aab7edd9032d4b489017cd17095f73803.png) . In other words,
. In other words, 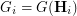 , where
, where 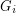 is the contracted graph and
is the contracted graph and 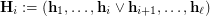 . In fact, the procedure
. In fact, the procedure 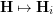 preserves completeness of
preserves completeness of  , as
, as 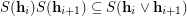 . Equivalently, the procedure
. Equivalently, the procedure 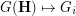 preserves rearrangeability of
preserves rearrangeability of 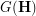 .
.
Counterexamples
Although the presented graph-theoretic statement ( ) of Problem (
) of Problem ( ) may look more complex, it provides somewhat more intuitive framework to study the problem and, in particular, Beneš conjecture. To illustrate this, let us now reconsider in terms of this framework and in more detail the 3 counterexamples for some extensions of Beneš conjecture discussed here.
) may look more complex, it provides somewhat more intuitive framework to study the problem and, in particular, Beneš conjecture. To illustrate this, let us now reconsider in terms of this framework and in more detail the 3 counterexamples for some extensions of Beneš conjecture discussed here.
Counterexample 1. The condition of simplicity of the graph  (essentially missing in the original statement [B75] of Beneš conjecture) is necessary for Conjecture (
(essentially missing in the original statement [B75] of Beneš conjecture) is necessary for Conjecture ( ). To see this, consider the following 2-stage 3-regular non-simple ordered graph
). To see this, consider the following 2-stage 3-regular non-simple ordered graph  :
:

Whereas 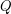 is obviously externally connected, the graph
is obviously externally connected, the graph 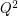 is not rearrageable. This is because it is evidently impossible to connect the two red vertices in
is not rearrageable. This is because it is evidently impossible to connect the two red vertices in 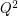 (a source and a target) with 3 mutually edge-disjoint plain paths.
(a source and a target) with 3 mutually edge-disjoint plain paths.
Counterexample 2. Conjecture ( ) is not directly generalizable to non-uniform graphs. More precisely, the condition of uniformity of
) is not directly generalizable to non-uniform graphs. More precisely, the condition of uniformity of 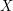 is necessary for the following reformulation of (
is necessary for the following reformulation of ( ):
):
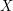 be a simple quasi-regular ordered multistage graph. Suppose that
be a simple quasi-regular ordered multistage graph. Suppose that 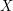 is uniform and externally connected. Then the graph
is uniform and externally connected. Then the graph 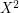 is rearrangeable.
is rearrangeable. Here 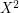 denotes the proper concatenation of 2 identical copies of
denotes the proper concatenation of 2 identical copies of 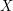 . To see the necessity, consider the following simple 4-stage 2-quasi-regular non-uniform ordered graph
. To see the necessity, consider the following simple 4-stage 2-quasi-regular non-uniform ordered graph 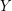 :
:
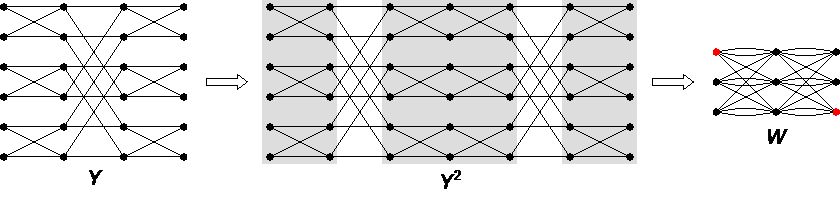
Whereas 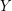 is obviously externally connected, the graph
is obviously externally connected, the graph 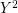 is not rearrangeable. To see this, recall that contracting all edges between two consecutive parts in a straight multistage graph preserves its rearrangeability. Therefore, if
is not rearrangeable. To see this, recall that contracting all edges between two consecutive parts in a straight multistage graph preserves its rearrangeability. Therefore, if 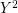 were rearrangeable then so would be the 3-stage graph
were rearrangeable then so would be the 3-stage graph  obtained from
obtained from 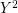 by contracting all edges in the shadowed areas. However, this is not true as it is evidently impossible to connect the two red vertices in
by contracting all edges in the shadowed areas. However, this is not true as it is evidently impossible to connect the two red vertices in 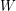 (a source and a target) with 4 mutually edge-disjoint plain paths.
(a source and a target) with 4 mutually edge-disjoint plain paths.
Counterexample 3. The stronger version of Conjecture ( ) (proposed essentially in the same paper [B75]), claiming that
) (proposed essentially in the same paper [B75]), claiming that 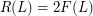 , is false. The graph
, is false. The graph  shown in Fig.1 is a counterexample as
shown in Fig.1 is a counterexample as 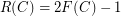 .
.
More information on Problem ( ) and Conjecture (
) and Conjecture ( ) can be found here (via Problem (
) can be found here (via Problem ( ) and Beneš conjecture).
) and Beneš conjecture).
Bibliography
*[B75] V.E. Beneš, Proving the rearrangeability of connecting networks by group calculation, Bell Syst. Tech. J. 54 (1975), 421-434.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University