We see that the eigenvalue of the eigenfunction is given by
for an appropriately chosen . Thus we need only actually consider , which we from now on denote . Then some calculation gives us that the integral is
We can show that (and this will suffice) that when is near ,
Solution (continued)
We see that the eigenvalue of the eigenfunction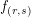 is given by
is given by
for an appropriately chosen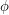 . Thus we need only actually consider
. Thus we need only actually consider 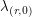 , which we from now on denote
, which we from now on denote 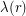 . Then some calculation gives us that the integral is
. Then some calculation gives us that the integral is
We can show that (and this will suffice) that when is near
is near 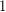 ,
,