Home » Subject » Graph Theory » Topological G.T.
Importance: Medium ✭✭
Author(s): Abertson, Michael O.
Berman, David M.
Subject: Graph Theory
» Topological Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 4th, 2013
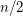Conjecture   Every planar graph on $ n $ verices has an induced forest with at least $ n/2 $ vertices.

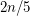This conjecture is best possible. (See [AW]). It follows from Borodin's theorem stating that every planar graph has an acyclic $ 5 $-colouring that every planar graph on $ n $ verices has an induced forest with at least $ 2n/5 $ vertices. The conjecture holds for planar graph with girth at least $ 5 $, because they can be partitionned into a stable set and a forest [BG] (see also [KT]).

Akiyama-Watanabe [AW] conjectured an even larger induced forest for bipartite planar graphs.

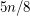Conjecture   Every bipartite planar graph on $ n $ verices has an induced forest with at least $ 5n/8 $ vertices.

This conjecture is also best possible. (See [AW]).

Bibliography

*[AB] M. O. Albertson and D. M. Berman. A conjecture on planar graphs. Graph Theory and Related Topics (J. A. Bondy and U. S. R. Murty, eds.), (Academic Press, 1979), 357.

[AW] J. Akiyama and M. Watanabe. Maximum induced forests of planar graphs. Graphs and Combinatorics 3 (1987), 201--202.

[B] O. V. Borodin. A proof of B. Grünbaum's conjecture on the acyclic 5-colorability of planar graphs. (Russian) Dokl. Akad. Nauk SSSR 231 (1976), no. 1, 18--20.

[BG] O. V. Borodin and A. N. Glebov. On the partition of a planar graph of girth 5 into an empty graph and an acyclic subgraph. Diskretn. Anal. Issled. Oper. Ser. 1 8:34–53, 2001

[KT] K. Kawarabayashi and C. Thomassen. Decomposing a planar graph of girth 5 into an independent set and a forest. Journal of Combinatorial Theory, Series B 99(4):674–684, 2009.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options