 login/create account
login/create account
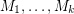 are matroids on
are matroids on  and
and 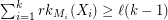 for every partition
for every partition  of
of  , then there exists
, then there exists 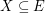 with
with 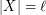 which is independent in every
which is independent in every 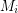 .
. Let us begin by stating two classic results. For a graph (or hypergraph) we let  denote the size of the smallest (vertex) cover and we let
denote the size of the smallest (vertex) cover and we let  denote the size of the largest matching.
denote the size of the largest matching.
 for every bipartite graph.
for every bipartite graph. 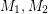 are matroids on
are matroids on  and
and  for every partition
for every partition 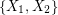 of
of  , then there exists
, then there exists 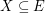 with
with 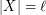 which is independent in both
which is independent in both 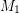 and
and 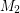 .
. The matroid intersection theorem is exactly the 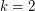 case of the above conjecture, but it may also be viewed as a generalization of König's theorem. To see this, let
case of the above conjecture, but it may also be viewed as a generalization of König's theorem. To see this, let  be a bipartite graph with edge set
be a bipartite graph with edge set  and bipartition
and bipartition 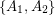 and for
and for 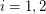 let
let 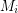 be the (uniform) matroid on
be the (uniform) matroid on  where a subset
where a subset 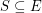 is independent if no two edges in
is independent if no two edges in  share an endpoint in
share an endpoint in 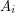 . Then
. Then 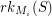 is the number of vertices in
is the number of vertices in 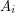 which are incident with an edge in
which are incident with an edge in  , so
, so 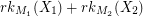 has minimum value
has minimum value  , and a set of edges is independent in both
, and a set of edges is independent in both 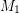 and
and 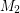 if and only if it is a matching, so the size of the largest such set is
if and only if it is a matching, so the size of the largest such set is  .
.
A famous conjecture of Ryser suggests a generalization of König's theorem to hypergraphs. It claims that every  -partite
-partite  -uniform hypergraph satisfies
-uniform hypergraph satisfies 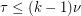 . The above conjecture is the common generalization of this conjecture of Ryser and the matroid intersection theorem. Aharoni [A] proved the 3-partite 3-uniform case of Ryser's conjecture, and this was extended by Aharoni-Berger [AB] to the
. The above conjecture is the common generalization of this conjecture of Ryser and the matroid intersection theorem. Aharoni [A] proved the 3-partite 3-uniform case of Ryser's conjecture, and this was extended by Aharoni-Berger [AB] to the 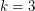 case of the above conjecture. The conjecture remains open for
case of the above conjecture. The conjecture remains open for 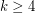 .
.
Bibliography
[A] R. Aharoni, Ryser's conjecture for tripartite 3-graphs, Combinatorica 21 (2001), 1-4. MathSciNet
*[AB] R. Aharoni, E. Berger, The intersection of a matroid with a simplicial complex. Trans. Amer. Math. Soc. 358 (2006), no. 11 MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University