Consider the circuit to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color. Then and are colored with the same color (color 2) in the second cycle covering them, and similarly and have the same color (color 3) in the second cycle covering them. (As otherwise is colored twice by the cycle which, if allowed, quickly shows necessity of 6 colors)
login/create account
Drupal
CSI of Charles University
Explanation of the 3-connected counterexample
Consider the circuit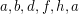
to be color 1. And assume there is a 5-cycle cover containing this circuit as one of the cycles. We distinguish the cycles by color.
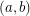and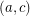 
are colored with the same color (color 2) in the second cycle covering them, and similarly 
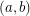and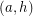 
have the same color (color 3) in the second cycle covering them. (As otherwise 
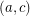is colored twice by the cycle 
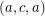which, if allowed, quickly shows necessity of 6 colors)
Then