 login/create account
login/create account
 has a dominating set of size
has a dominating set of size 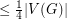 .
. Motivated by some problems in multigrid computations, Matheson and Tarjan [MT] considered the problem of finding small dominating sets in plane triangulations. They proved that every such graph  has a dominating set of size
has a dominating set of size 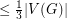 and posed the above question.
and posed the above question.
The Octahedron is a triangulation with 6 vertices for which every dominating set has size 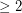 , so no constant better than
, so no constant better than 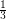 can be achieved in general. However, it appears that one can do better for larger graphs. The most extreme examples here (also from [MT]) are constructed as follows: Start with
can be achieved in general. However, it appears that one can do better for larger graphs. The most extreme examples here (also from [MT]) are constructed as follows: Start with  disjoint copies of
disjoint copies of 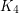 embedded in the plane, and then add edges to complete this graph to a triangulation (with
embedded in the plane, and then add edges to complete this graph to a triangulation (with 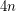 vertices). Now each of the original copies of
vertices). Now each of the original copies of 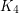 has an inner vertex which has degree 3 in the final graph, and in order to cover it, one must take at least one vertex from this
has an inner vertex which has degree 3 in the final graph, and in order to cover it, one must take at least one vertex from this 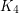 . It follows that every dominating set has size
. It follows that every dominating set has size 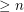 .
.
Since the Matheson-Tarjan proof is short and instructive, we sketch it here. In fact, we shall prove (as they did) the stronger statement that every near-triangulation (a graph embedded in the plane with all finite faces of size three) has a (possibly improper) 3-coloring so that each color class is a dominating set and so that the subgraph induced by those vertices incident with the infinite face is properly colored. This stronger fact we prove by induction. If the infinite face is not bounded by a cycle or the infinite face is bounded by a cycle which has a chord, then the graph may be written as the union of two near-triangulations 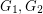 where
where 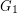 and
and 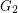 either share one vertex or two adjacent vertices and one edge. In either case, the result follows by applying induction to
either share one vertex or two adjacent vertices and one edge. In either case, the result follows by applying induction to 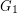 and
and 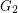 . Otherwise, choose a vertex
. Otherwise, choose a vertex  on the infinite face, delete
on the infinite face, delete  and apply induction. Since the neighbors of
and apply induction. Since the neighbors of  are all on the infinite face, and do not form an independent set, there are at least two colors, say
are all on the infinite face, and do not form an independent set, there are at least two colors, say 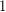 and
and  , which appear on the neighbors of
, which appear on the neighbors of  . Now giving
. Now giving  the color
the color  gives a solution.
gives a solution.
Bibliography
[MT] L. R. Matheson, R. E. Tarjan, Dominating sets in planar graphs. European J. Combin. 17 (1996), no. 6, 565--568. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University