 login/create account
login/create account
Let 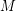 be a matroid of rank
be a matroid of rank  , and for
, and for 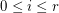 let
let 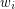 be the number of closed sets of rank
be the number of closed sets of rank  .
.
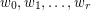 is unimodal.
is unimodal. 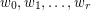 is log-concave.
is log-concave. A sequence 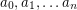 is log-concave if
is log-concave if 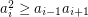 for all
for all 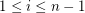 .
.
The first of these conjectures is due to Rota [R], the second is folklore as far as I (M. DeVos) know. The special case of proving the second conjecture for 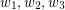 amounts to showing that
amounts to showing that 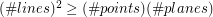 and has been called the points-lines-planes conjecture. Seymour [S] proved this conjecture in the special case where every line contains at most four points, but it is still open in general.
and has been called the points-lines-planes conjecture. Seymour [S] proved this conjecture in the special case where every line contains at most four points, but it is still open in general.
Bibliography
*[R] Rota, Gian-Carlo, Combinatorial theory, old and new. Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 3, pp. 229--233. Gauthier-Villars, Paris, 1971. MathSciNet
[S] Seymour, P. D. On the points-lines-planes conjecture, J. Combin. Theory Ser. B 33 (1982), no. 1, 17--26. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University