 login/create account
login/create account
 there exists a vertex transitive graph
there exists a vertex transitive graph  whose matching polynomial has a root of multiplicity at least
whose matching polynomial has a root of multiplicity at least  .
. Let  be a graph of order
be a graph of order  . Denote by
. Denote by 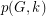 the number of
the number of  -matchings in
-matchings in  . The matching polynomial of
. The matching polynomial of  is defined as
is defined as 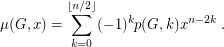 It is known that every matching polynomial has only real roots. See [HL, GG].
It is known that every matching polynomial has only real roots. See [HL, GG].
It would be interesting to solve the Conjecture even for 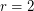 , that is to find a vertex transitive graph whose matching polynomial has a nonsimple root. Such a graph would not have a hamiltonian path (see [HL, GG]), thus giving a negative answer to a problem of Lovász.
, that is to find a vertex transitive graph whose matching polynomial has a nonsimple root. Such a graph would not have a hamiltonian path (see [HL, GG]), thus giving a negative answer to a problem of Lovász.
This conjecture is false.
 and a root
and a root 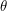 of
of 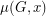 , a vertex
, a vertex  of
of  is said to be
is said to be 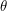 -essential if the multiplicity of
-essential if the multiplicity of 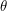 as a root of
as a root of 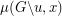 is one less than the multiplicity of
is one less than the multiplicity of 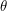 as a root of
as a root of 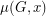 .
. In [K], Ku and Chen prove the following analogue of Gallai's Lemma.
 be a graph and
be a graph and 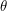 be a root of
be a root of 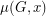 . If all vertices of
. If all vertices of  are
are 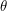 -essential, then
-essential, then 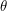 has multiplicity 1 as a root of
has multiplicity 1 as a root of 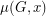 .
. Since every graph contains a 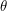 -essential vertex, all vertices of a vertex-transitive graph are
-essential vertex, all vertices of a vertex-transitive graph are 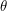 -essential. Thus the matchings polynomial of any vertex-transitive graph has only simple roots.
-essential. Thus the matchings polynomial of any vertex-transitive graph has only simple roots.
Bibliography
[HL] O. J. Heilmann, E. H. Lieb, Theory of monomer-dimer systems, Comm. Math. Phys. 25 (1972), 190-232. MathSciNet
[GG] C. D. Godsil, I. Gutman, On the theory of the matching polynomial, J. Graph Theory 5 (1981), 137-144. MathSciNet
[K] Cheng Yeaw Ku and William Chen, An Analogue of the Gallai-Edmunds Structure Theorem for Nonzero Roots of the Matchings Polynomial (June 2008). Preprint available from arXiv
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University