Home » Subject » Graph Theory » Probabilistic G.T.
Importance: Medium ✭✭
Author(s): Pemantle, Robin
Subject: Graph Theory
» Probabilistic Graph Theory
Keywords: forest
negative association
Recomm. for undergrads: no
Posted by: mdevos
on: June 30th, 2008
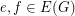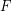Conjecture   Let $ G $ be a finite graph, let $ e,f \in E(G) $, and let $ F $ be the edge set of a forest chosen uniformly at random from all forests of $ G $. Then \[ {\mathbb P}(e \in F \mid f \in F}) \le {\mathbb P}(e \in F) \]

The FKG inequality is the cornerstone of a respectable theory of positive association; If a natural lattice condition holds, we can use it to deduce positive association. On the other hand, the theory of negative associations is still lacking good techniques. See Pemantle's lovely paper [P] for an excellent description of this situation. The conjecture highlighted above seems to be almost obviously true, but we have no tools to prove it.

Modifying the conjecture by replacing "forest" by "spanning tree" gives a true statement which was proved by Feder and Mihail [FM]. Actually, they prove that this holds more generally for uniform bases of balanced matroids. Perhaps surprisingly, this is false for general matroids, see [SW].

Bibliography

[FM] T. Feder and M. Mihail, Balanced Matroids. Proc 24th Annual STOC 26 - 38 (1992).

*[P] R. Pemantle, Towards a theory of negative dependence, Journal of Mathematical Physics 41 (2000), 1371–1390.

[SW] P. D. Seymour and D. J. A. Welsh, Combinatorial applications of an inequality from statistical mechanics. Math. Proc. Camb. Phil. Soc. 77 485 - 495 (1975).


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options