 login/create account
login/create account
 , there exists a constant
, there exists a constant 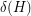 , so that every graph
, so that every graph  without an induced subgraph isomorphic to
without an induced subgraph isomorphic to  contains either a clique or an independent set of size
contains either a clique or an independent set of size 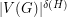 .
. There are numerous interesting classes of graphs which are based upon forbidding one or more induced subgraphs. For instance: chordal graphs, split graphs, and claw-free graphs. Numerous other natural classes of graphs have been proved to have such characterizations, most famously perfect graphs, but also line graphs and comparability graphs. All of these classes are very well structured (far from random) and their members all either have large cliques or independent sets. On the flip side of this are random graphs. It is well known that a random graph on  vertices has both clique and independence number highly concentrated around
vertices has both clique and independence number highly concentrated around 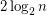 . The Erdos-Hajnal conjecture suggests a fundamental separation between these two worlds in terms of independence/clique sizes.
. The Erdos-Hajnal conjecture suggests a fundamental separation between these two worlds in terms of independence/clique sizes.
Erdös and Hajnal proved that this conjecture is true for the recursive class of graphs 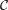 defined as follows. The one vertex graph is in
defined as follows. The one vertex graph is in 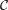 , and if
, and if 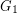 and
and 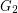 lie in
lie in 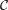 , then the disjoint union of
, then the disjoint union of 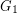 and
and 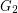 lies in
lies in 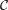 , as does the graph obtained from the disjoint union by adding an edge between
, as does the graph obtained from the disjoint union by adding an edge between 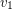 and
and 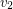 for every
for every 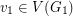 and
and 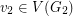 . More generally, Alon, Pach, and Solymosi proved that if
. More generally, Alon, Pach, and Solymosi proved that if 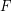 is a graph with
is a graph with 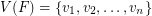 for which the Erdös-Hajnal conjecture holds, and
for which the Erdös-Hajnal conjecture holds, and  are graphs for which the Erdos-Hajnal conjecture holds, then the graph obtained from
are graphs for which the Erdos-Hajnal conjecture holds, then the graph obtained from 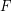 by blowing up each vertex
by blowing up each vertex 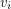 with a copy of
with a copy of 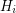 (more precisely, starting from the disjoint union of
(more precisely, starting from the disjoint union of 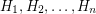 , we add all possible edges between the vertices of
, we add all possible edges between the vertices of 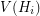 and
and 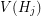 if
if 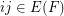 ) also satisfies the Erdos-Hajnal conjecture.
) also satisfies the Erdos-Hajnal conjecture.
The Erdös-Hajnal property is known to hold for a number of small graphs (and using the above result this may be easily bootstrapped). For instance, the conjecture is known to hold when  is a path of three edges, and recently M. Chudnovsky and S. Safra have announced a proof when
is a path of three edges, and recently M. Chudnovsky and S. Safra have announced a proof when  is a bull (a triangle plus two pendant edges). However, our knowledge here is still quite limited. In particular, Lovasz has suggested the following very special case which remains open.
is a bull (a triangle plus two pendant edges). However, our knowledge here is still quite limited. In particular, Lovasz has suggested the following very special case which remains open.
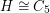 ?
? Bibliography
[APS] N. Alon, J. Pach, and J. Solymosi, Ramsey-type theorems with forbidden subgraphs, Combinatorica 21 (2001), 155-170.
[EH] P. Erdös and A. Hajnal, Ramsey-type theorems, Discrete Appl. Math. 25 (1989), 37-52 MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University