 login/create account
login/create account
Osthus, Deryk
Simultaneous partition of hypergraphs ★★
Problem Let  and
and 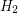 be two
be two  -uniform hypergraph on the same vertex set
-uniform hypergraph on the same vertex set 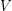 . Does there always exist a partition of
. Does there always exist a partition of 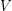 into
into  classes
classes  such that for both
such that for both 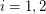 , at least
, at least 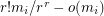 hyperedges of
hyperedges of 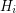 meet each of the classes
meet each of the classes  ?
?
 and
and 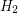 be two
be two  -uniform hypergraph on the same vertex set
-uniform hypergraph on the same vertex set 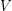 . Does there always exist a partition of
. Does there always exist a partition of 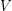 into
into  classes
classes  such that for both
such that for both 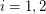 , at least
, at least 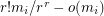 hyperedges of
hyperedges of 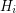 meet each of the classes
meet each of the classes  ?
? Keywords:
Complexity of the H-factor problem. ★★
An  -factor in a graph
-factor in a graph  is a set of vertex-disjoint copies of
is a set of vertex-disjoint copies of  covering all vertices of
covering all vertices of  .
.
Problem Let  be a fixed positive real number and
be a fixed positive real number and  a fixed graph. Is it NP-hard to determine whether a graph
a fixed graph. Is it NP-hard to determine whether a graph  on
on  vertices and minimum degree
vertices and minimum degree  contains and
contains and  -factor?
-factor?
 be a fixed positive real number and
be a fixed positive real number and  a fixed graph. Is it NP-hard to determine whether a graph
a fixed graph. Is it NP-hard to determine whether a graph  on
on  vertices and minimum degree
vertices and minimum degree  contains and
contains and  -factor?
-factor?
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University