 login/create account
login/create account
Kimberling, Clark
Special M ★★
Author(s): Kimberling
Let  denote the golden ratio,
denote the golden ratio, 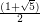 and let
and let  denote the floor function. For fixed
denote the floor function. For fixed  , let
, let 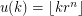 , let
, let  , and let
, and let 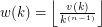 . We can expect
. We can expect  to have about the same growth rate as
to have about the same growth rate as  .
.
Conjecture Prove or disprove that for every fixed 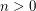 , as
, as  ranges through all the positive integers, there is a number
ranges through all the positive integers, there is a number  such that
such that 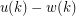 takes each of the values
takes each of the values 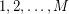 infinitely many times, and
infinitely many times, and 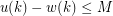 . (Can you formulate
. (Can you formulate  as a function of
as a function of  ? Generalize for other numbers
? Generalize for other numbers  ?)
?)
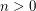 , as
, as  ranges through all the positive integers, there is a number
ranges through all the positive integers, there is a number  such that
such that 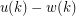 takes each of the values
takes each of the values 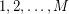 infinitely many times, and
infinitely many times, and 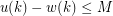 . (Can you formulate
. (Can you formulate  as a function of
as a function of  ? Generalize for other numbers
? Generalize for other numbers  ?)
?) Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University