 login/create account
login/create account
general position subset, no-three-in-line problem
General position subsets ★★
Author(s): Gowers
Question What is the least integer 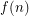 such that every set of at least
such that every set of at least 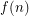 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)?
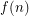 such that every set of at least
such that every set of at least 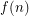 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University