 login/create account
login/create account
Frobenius, Ferdinand G.
Subgroup formed by elements of order dividing n ★★
Author(s): Frobenius
Conjecture
Suppose  is a finite group, and
is a finite group, and  is a positive integer dividing
is a positive integer dividing 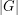 . Suppose that
. Suppose that  has exactly
has exactly  solutions to
solutions to 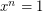 . Does it follow that these solutions form a subgroup of
. Does it follow that these solutions form a subgroup of  ?
?
Keywords: order, dividing

 Drupal
Drupal CSI of Charles University
CSI of Charles University