 login/create account
login/create account
Euler, Leonhard P.
A sextic counterexample to Euler's sum of powers conjecture ★★
Author(s): Euler
Problem Find six positive integers 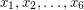 such that
such that 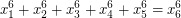 or prove that such integers do not exist.
or prove that such integers do not exist.
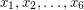 such that
such that 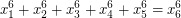 or prove that such integers do not exist.
or prove that such integers do not exist. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University