 login/create account
login/create account
Essential singularity
Something like Picard for 1-forms ★★
Author(s): Elsner
Conjecture Let  be the open unit disk in the complex plane and let
be the open unit disk in the complex plane and let 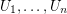 be open sets such that
be open sets such that 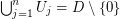 . Suppose there are injective holomorphic functions
. Suppose there are injective holomorphic functions 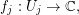
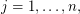 such that for the differentials we have
such that for the differentials we have 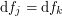 on any intersection
on any intersection 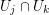 . Then those differentials glue together to a meromorphic 1-form on
. Then those differentials glue together to a meromorphic 1-form on  .
.
 be the open unit disk in the complex plane and let
be the open unit disk in the complex plane and let 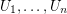 be open sets such that
be open sets such that 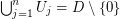 . Suppose there are injective holomorphic functions
. Suppose there are injective holomorphic functions 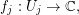
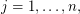 such that for the differentials we have
such that for the differentials we have 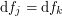 on any intersection
on any intersection 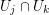 . Then those differentials glue together to a meromorphic 1-form on
. Then those differentials glue together to a meromorphic 1-form on  .
. Keywords: Essential singularity; Holomorphic functions; Picard's theorem; Residue of 1-form; Riemann surfaces

 Drupal
Drupal CSI of Charles University
CSI of Charles University