 login/create account
login/create account
coding
The robustness of the tensor product ★★★
Author(s): Ben-Sasson; Sudan
Problem Given two codes 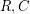 , their Tensor Product
, their Tensor Product 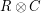 is the code that consists of the matrices whose rows are codewords of
is the code that consists of the matrices whose rows are codewords of 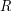 and whose columns are codewords of
and whose columns are codewords of  . The product
. The product 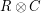 is said to be robust if whenever a matrix
is said to be robust if whenever a matrix  is far from
is far from 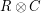 , the rows (columns) of
, the rows (columns) of  are far from
are far from 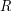 (
( , respectively).
, respectively).
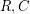 , their Tensor Product
, their Tensor Product 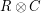 is the code that consists of the matrices whose rows are codewords of
is the code that consists of the matrices whose rows are codewords of 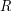 and whose columns are codewords of
and whose columns are codewords of  . The product
. The product 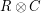 is said to be robust if whenever a matrix
is said to be robust if whenever a matrix  is far from
is far from 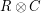 , the rows (columns) of
, the rows (columns) of  are far from
are far from 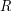 (
( , respectively).
, respectively).
The problem is to give a characterization of the pairs 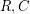 whose tensor product is robust.
whose tensor product is robust.
Keywords: codes; coding; locally testable; robustness

 Drupal
Drupal CSI of Charles University
CSI of Charles University