 login/create account
login/create account
algebraic independence
Schanuel's Conjecture ★★★★
Author(s): Schanuel
Conjecture Given any  complex numbers
complex numbers 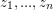 which are linearly independent over the rational numbers
which are linearly independent over the rational numbers 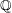 , then the extension field
, then the extension field 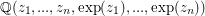 has transcendence degree of at least
has transcendence degree of at least  over
over 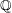 .
.
 complex numbers
complex numbers 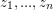 which are linearly independent over the rational numbers
which are linearly independent over the rational numbers 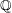 , then the extension field
, then the extension field 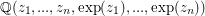 has transcendence degree of at least
has transcendence degree of at least  over
over 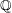 .
. Keywords: algebraic independence

 and
and  are
are  Drupal
Drupal CSI of Charles University
CSI of Charles University