 login/create account
login/create account
A diagram about funcoids and reloids ★★
Author(s): Porton
Define for posets with order  :
:
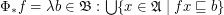 ;
;
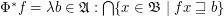 .
.
Note that the above is a generalization of monotone Galois connections (with  and
and  replaced with suprema and infima).
replaced with suprema and infima).
Then we have the following diagram:
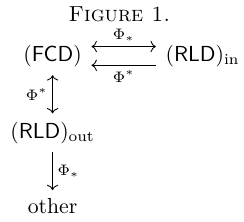
What is at the node "other" in the diagram is unknown.
Conjecture "Other" is 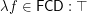 .
.
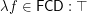 .
. Question What repeated applying of 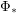 and
and 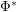 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 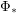 and/or
and/or 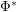 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets?
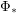 and
and 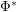 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 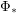 and/or
and/or 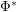 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets? Keywords: Galois connections
Outward reloid of composition vs composition of outward reloids ★★
Author(s): Porton
Conjecture For every composable funcoids  and
and 
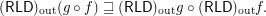
 and
and 
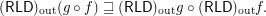
Keywords: outward reloid
A funcoid related to directed topological spaces ★★
Author(s): Porton
Conjecture Let 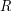 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 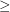 be the order on this set. Then
be the order on this set. Then 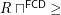 is a complete funcoid.
is a complete funcoid.
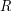 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 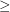 be the order on this set. Then
be the order on this set. Then 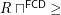 is a complete funcoid.
is a complete funcoid. Proposition It is easy to prove that 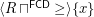 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
.
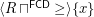 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
. If proved true, the conjecture then can be generalized to a wider class of posets.
Keywords:
Infinite distributivity of meet over join for a principal funcoid ★★
Author(s): Porton
Conjecture 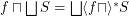 for principal funcoid
for principal funcoid  and a set
and a set  of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations.
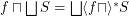 for principal funcoid
for principal funcoid  and a set
and a set  of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations. Keywords: distributivity; principal funcoid
Entourages of a composition of funcoids ★★
Author(s): Porton
Conjecture 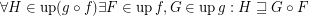 for every composable funcoids
for every composable funcoids  and
and  .
.
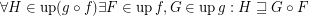 for every composable funcoids
for every composable funcoids  and
and  .
. Keywords: composition of funcoids; funcoids

 Drupal
Drupal CSI of Charles University
CSI of Charles University