 login/create account
login/create account
If  is a graph and
is a graph and ![$ p \in [0,1] $](/files/tex/1d076f7332523eb59bd7deae19667f83f0a3b6e0.png) , we let
, we let  denote a subgraph of
denote a subgraph of  where each edge of
where each edge of  appears in
appears in  with independently with probability
with independently with probability 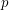 .
.
Problem Does there exist a constant  so that
so that 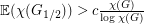 ?
?
 so that
so that 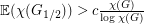 ?
? It is a classical result that the above problem has a positive answer when  is the complete graph. More generally, the lower bound
is the complete graph. More generally, the lower bound  is known.
is known.
It is easy to obtain the bound 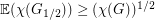 , since we may imagine forming two random subgraphs
, since we may imagine forming two random subgraphs 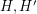 of
of  by putting each edge of
by putting each edge of  in either
in either  or
or 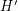 independently with probability
independently with probability 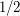 . Then
. Then 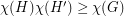 and this gives the desired bound. A similar argument with three subgraphs shows that
and this gives the desired bound. A similar argument with three subgraphs shows that 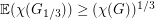 , however these arguments all seem to require integer multiples, so the best known lower bound on
, however these arguments all seem to require integer multiples, so the best known lower bound on 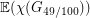 of this form is
of this form is 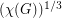 .
.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University