Home » Subject » Analysis
Importance: High ✭✭✭
Author(s):
Subject: Analysis
Keywords: subspace
Recomm. for undergrads: no
Posted by: tchow
on: February 9th, 2009
Problem   Does every bounded linear operator on an infinite-dimensional separable Hilbert space have a non-trivial closed invariant subspace?

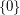Let $ H $ be a Hilbert space. The subspaces $ \{0\} $ and $ H $ are trivially invariant under any linear operator on $ H $, and so these are referred to as the trivial invariant subspaces. The problem is concerned with determining whether bounded operators necessarily have non-trivial invariant subspaces.

This is one of the most famous open problems in functional analysis. Enflo [1] constructed Banach spaces for which the corresponding question has a negative answer, and recently Argyros and Haydon constructed a Banach space for which the corresponding question has a positive answer [4].

For a nice overview to the problem see [2], [3] or [5].

Bibliography

[1] P. Enflo, On the invariant subspace problem for Banach spaces, Acta Math. 158 (1987), 213-313. MathSciNet

[2] B. S. Yadav, The Present State and Heritages of the Invariant Subspace Problem, Milan J. Math. 73 (2005), 289-316. MathSciNet another link

[3] H. Radjavi and P. Rosenthal, The Invariant Subspace Problem, The Mathematics Intelligencer 4 (1982), no. 1, 33-37. MathSciNet

[4] S. A. Argyros and R. G. Haydon, A hereditarily indecomposable 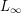$ L_\infty $-space that solves the scalar-plus-compact problem, arXiv:0903.3921 (2009).

[5] J. Noel. The Invariant Subspace Problem. Honours Thesis, Thompson Rivers University. Link to pdf.


* indicates original appearance(s) of problem.
2 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options