 login/create account
login/create account
Subset-sums equality (pigeonhole version)
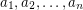 be natural numbers with
be natural numbers with 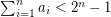 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 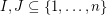 with
with 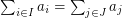 . Is it possible to find such a pair
. Is it possible to find such a pair 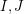 in polynomial time?
in polynomial time? This is one of a class of search problems for which a positive solution is garaunteed (so the corresponding decision problem is trivial) based on a theoretical property of the problem. Another such problem is given a Hamiltonian cycle in a cubic graph, find a second Hamiltonian cycle (here a theorem of Smith guarantee's a positive solution). The above problem is particularly attractive, since the proof that a pair 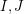 must exist is quite simple, but it gives no insight into how to find the pair
must exist is quite simple, but it gives no insight into how to find the pair 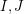 .
.
It seems to be consensus among the cryptography community that this problem is hard.
You're right
I finally located a copy of the paper on the author's web page at http://www.lri.fr/~santha/ (why didn't that occur to me before?), and it's much clearer to me now--you're absolutely right. I guess the one suggestion I would make is to adopt their terminology and include the term 'pigeonhole' in the name of the problem to distinguish this variation from the more general case.
How's this?
I am quite certian I have seen this problem called simply "subset-sums equality" before, so I have just appended "(pigeonhole version)" to the title. I hope that this is increasing the clarity.
I think it is still open
First a disclaimer: I am no expert on this problem.. I heard it awhile ago, liked it, wrote it down, and that's what you see here. However, I do believe it is still open. If my understanding is correct, the problem considered in the paper you mention ("Efficient approximation algorithms for the subset-sums equality problem" by Bazgan, Santha and Tuza, JCSS Vol.64 Issue 2, March 2002) is a relaxed version of the one stated here where the restriction 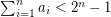 is not present, and the goal is to find a pair of nonempty disjoint subsets
is not present, and the goal is to find a pair of nonempty disjoint subsets 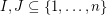 so that
so that  and
and 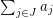 are as close as possible. I believe the only hardness results they obtain are for this problem.
are as close as possible. I believe the only hardness results they obtain are for this problem.
The thing still missing is what to do with the funny assumption 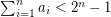 . Although the problem is a search problem which looks roughly like a knapsack-type problem (and thus should be NP-hard), the associated decision problem is trivially "true", yet there is no obvious way to use this information.
. Although the problem is a search problem which looks roughly like a knapsack-type problem (and thus should be NP-hard), the associated decision problem is trivially "true", yet there is no obvious way to use this information.
PS: thanks for the post!
A little more
Just an afterthought to my previous comment... Even if this problem is known not to be computable in polynomial time, it would still be interesting to know if it is NP-hard or not.
Re: A little more
Problems with guaranteed-to-exist solutions (like this one, & others in PPA, PPAD, etc.) are not NP-complete unless NP = coNP and the Polynomial Hierarchy collapses. Now, we don't yet know that P != NP, or even that P != PH.
Re: A little more
Yes, I made that comment before I read the paper by Bazgan, Santha and Tuza. They mentioned in passing that the problem isn't NP-hard unless NP = coNP, and apparently felt that it was obvious enough to not require any further comment. I'm probably missing something obvious, but I can't quite follow this. With factorization (for example), a number's prime decomposition is unique and can serve as a certificate for both 'yes' and 'no' instances. For pigeonhole subset-sums equality, the solutions are not necessarily unique. It would depend on exactly how one crafted the corresponding decision problem, but it's not clear to me what the certificate would be for a 'no' instance.
Should this problem still be considered open?
I was doing a quick search for background on this question and came across this article: http://dx.doi.org/10.1006/jcss.2001.1784 , "Efficient approximation algorithms for the subset-sums equality problem" by Bazgan, Santha and Tuza, JCSS Vol.64 Issue 2 (March 2002). I only have access to the abstract, so I might be misinterpreting this, but they say, "... On the other hand, we show that in the case where the value of a solution is the positive difference between the two partial sums, the problem is not 2nk -approximable in polynomial time unless P = NP, for any constant k." I take this to mean that there are no exact polynomial time algorithms unless P=NP. If so, this problem is only open in the sense that any question reducible to P vs. NP can be considered open.
Problem formulation
It seems to me that there are some typos in the problem formulation. The sum should be less than 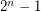 . The subsets should be nonempty.
. The subsets should be nonempty.
- JS

 Drupal
Drupal CSI of Charles University
CSI of Charles University
The problems are in PPP and PPA, respectively
Both this problem and the Smith/2nd Hamiltonian Path problems were suggested by Papadimitriou in his 1991 paper 'On the Complexity of the Parity Argument and Other Inefficient Proofs of Existence". (See http://www.cs.berkeley.edu/~christos/papers/ for a copy of the journal version.)
These problems are in natural complexity classes related to though apparently somewhat larger than PPAD . The subset sum problem is in the class PPP and the Smith problem is in the class PPA. Neither is known to be complete for the respective complexity class as far as I know.